[Python.MatPlotLib] Boston Housing Price Dataset 종합 실습 (plot, subplot, StandardScaler, boxplot, Correlation Matrix)
2021. 1. 17. 05:00ㆍPython과 머신러닝/MatPlotLib 데이터 시각화
1. Data Input과 Data 형태 1차 분석
In [1]:import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
In [2]:data_url = 'HousingData.csv' #https://www.kaggle.com/altavish/boston-housing-dataset
df_data = pd.read_csv(data_url)
df_data.head()
Out[2]:
- Boston Housing Price Dataset을 사용하여 종합 실습을 해보자.
- df_data.head를 통해 데이터에 어떤 값들이 있는지 한번 쭉 살피면 좋다.
- 실제 데이터는 kaggle에서 받을 수 있다.
2. NaN값 확인 및 처리
In [3]:for i in range(df_data.shape[1]):
col = df_data.columns[i]
print(col, np.count_nonzero(np.isnan(df_data[col])), df_data[col].mean())
CRIM 20 3.6118739711934156
ZN 20 11.2119341563786
INDUS 20 11.083991769547332
CHAS 20 0.06995884773662552
NOX 0 0.5546950592885372
RM 0 6.284634387351788
AGE 20 68.51851851851852
DIS 0 3.795042687747034
RAD 0 9.549407114624506
TAX 0 408.2371541501976
PTRATIO 0 18.455533596837967
B 0 356.67403162055257
LSTAT 20 12.715432098765435
MEDV 0 22.532806324110698
In [4]:df_data = df_data.fillna(df_data.mean()) #na 값을 채우는데, 각 column의 min 값을 가져와서 채운다
df_data.head(10)
Out[4]:

- 데이터 전처리 중 가장 기본적인 단계는 NaN값 처리이다
- NaN값이 들어가면 데이터가 정상적으로 처리되지 않는 경우들이 종종 있어서, NaN값을 처리해야 한다
- 그 필요성을 확인하기 위해 In[3]의 동작을 수행해본다.
- Out[3]은 각 Column의 이름, NaN 값을 가진 요소 수, 그리고 평균값을 출력한다
- 그 이유는, NaN 값을 가진 Column이 있는지를 확인하고, 이를 평균 값으로 채운 뒤에 잘 채워졌는지 확인하기 위함이다.
- In[4]의 fillna함수는 Dataframe의 NaN값을 채워주는 함수이고, df_data.mean()을 parameter로 전달하면 각 Series의 평균값을 넣겠다는 의미가 된다.
- 그리하여 Out[4]의 CHAS, LSTAT에 mean 값이 담겨 있는 것을 확인할 수 있다.
3. 전체 데이터 plot
In [5]:df_data.plot()
Out[5]:
- df_data에 대한 plot을 하면 Out[5]와 같이 모든 데이터를 하나의 Plot으로 그려준다.
- 지금처럼 Series의 종류가 다양하고 각 Series의 scale이 맞지 않는다면 많은 것을 볼 수는 없지만, 특이점이 없는지를 보는 정도의 초도 분석으로는 의미가 있다.
- 한 번쯤은 .plot()으로 전체 그림을 보고 시작하면 도움이 된다.
4. Data 정규화 및 분포도 분석
In [9]:from sklearn.preprocessing import StandardScaler
std_scaler = StandardScaler()
scale_data = std_scaler.fit_transform(df_data)
scale_data
Out[9]:array([[-0.42232846, 0.29644292, -1.31101039, ..., 0.44105193, -1.10414593, 0.15968566],
[-0.41986984, -0.48963852, -0.5997709 , ..., 0.44105193, -0.51035272, -0.10152429],
[-0.41987219, -0.48963852, -0.5997709 , ..., 0.39642699, -1.23974774, 1.32424667],
..., [-0.41595175, -0.48963852, 0.1264106 , ..., 0.44105193, -1.00993835, 0.14880191],
[-0.41023216, -0.48963852, 0.1264106 , ..., 0.4032249 , -0.8900378 , -0.0579893 ],
[-0.41751548, -0.48963852, 0.1264106 , ..., 0.44105193, -0.69020355, -1.15724782]])
In [10]:fig=plt.figure()
ax=fig.add_subplot(1,1,1)
ax.boxplot(scale_data, labels=df_data.columns)

- 3단계에서 본것처럼 정규화가 되어있지 않는 데이터는 함께 보기가 어렵다.
- 그래서 정규화를 해야하는데, 고등학교 통계 시간에 배운 정보를 따라서 직접 정규화를 구현해도 좋지만, Scikit Learn에서 StandardScaler라는 정규화 모듈이 있다.
- In [9]는 정규화 모듈을 생성하고 fit_transfom 함수를 통해 정규화를 진행한다.
- 그 결과로 나온 scale_data는 기존 DataFrame을 각 Series별로 정규화하여 배열에 담아서 반환한다.
- 이 데이터를 boxplot으로 그려보면 각 변수들의 분포도를 확인할 수 있다.
- CRIM은 분포가 아주 낮아서 대부분 0에 가깝고 위로 outlier들이 존재한다는 것을 알 수 있다.
- 그에 비해 INDUS / RAD와 같은 값들은 넓게 분포되어 있고 이상치가 없다는 것을 알 수 있다.
5. 각 변수 분석
In [8]:df_data['AGE'].sort_values().reset_index(drop=True).plot(kind='line')
Out[8]: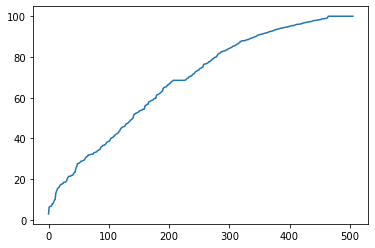
- In[8]은 각 변수를 시각적으로 이해하기 좋은 함수이다.
- Age라는 변수의 값들을 오름차순으로 정렬하여 (신식 -> 구식), x축은 요소의 번호/순서가 되고, y축은 각 요소의 Age값이 된다.
- 그렇기 때문에 중위값은 x축 250 정도의 y값을 확인하면 알 수 있고, 약 70 정도라는 것을 확인할 수 있다.
- Boston Housing Price Dataset에서 'Age'의 의미를 파악하니 '1940년 전에 지어진 집의 비율'이라고 정의하였고, 그래서 70이라는 값의 의미는 70%이 집이 1940년 전에 지어졌다는 것을 의미한다.
- 'Age'는 고르게 분포되어있다는 것을 확인할 수 있다.
In [11]:df_data['MEDV'].sort_values().reset_index(drop=True).plot()
Out[11]:
- MEDV는 집들의 중위값을 담는 Series이다.
- 마찬가지로 오름차순으로 쭉 정리를 해보니 0~50이라는 중위값을 다양하게 갖는 것을 볼 수 있다.
- 특이한 점은, 400번째 요소까지는 완만하게 오르던 집값이, 400 이후로는 급격하게 늘어나는 것을 볼 수 있다.
- 즉, 80%의 집들은 비슷한 값을 하고 있고, 나머지 20%의 집값이 매우 높은 것이다.
- 한국도 비슷하듯이, 비싼 집은 비싸서 더 인기가 늘고 아닌 집들은 완만한 가격 추세를 유지하는 것 같다.
- 대부분의 집들은 낮은 가격을 유지하고, 오른쪽에 긴 꼬리가 있을 것이라고 볼 수 있는 데이터이다.
6. 두 데이터 간의 상관관계
In [6]:df_data.plot(kind='scatter', x='AGE', y='MEDV')
Out[6]:
- 초도 분석이 끝나면 더 관심 있는 변수들의 상호관계를 분석할 수 있다.
- In[6]는 scatter plot(분포도)로 Age와 MEDV(Median Value, Boston 집값의 중앙값)을 보여주는 그래프이다.
- 이로 알 수 있는 건, 초고가의 집은 연식이 얼마 안 된 집에서 아주 오래된 집까지 전부 분포해 있지만 (그래프의 상단)
- 60년까지는 집값과 가격의 상관관계가 크지 않은 것처럼 보이고, 60년이 지난 후의 집들은 비교적 저렴한 것으로 보인다.
- 이는 집이 오래되면 가격이 떨어진다는 1차원적인 추론을 할 수도 있지만, 60년 전에는 인체에 해로운 성분을 많이 써서 선호도가 떨어질 수도 있고, 특정 동네에 먼저 집이 지어졌는데 동네에 대한 인식(범죄율 등)이 안 좋아서 그럴 수도 있기 때문에, 간단한 상관관계 정도로 파악하는 것이 적당할 듯하다.
7. Y변수와 여러 X변수들 간(1:N)의 상관관계 한 번에 그리기 (.scatter 함수)
In [7]:fig = plt.figure(figsize=(10,10))
ax = [] for i in range(1,5):
ax.append(fig.add_subplot(2,2,i))
columns = ['CRIM', 'PTRATIO', 'AGE', 'NOX'] #범죄율, 학생/교사 비율, 1940년 이전에 건축된 부동산의 비율 (높을수록 오래된 집), 농축 일산화질소 량
colors = ['b', 'g' ,'c', 'r']
for i in range(4):
ax[i].scatter(df_data[columns[i]],
df_data['MEDV'],
s=0.9,
color=colors[i],
label=columns[i])
ax[i].legend()
ax[i].set_title(columns[i])
plt.subplots_adjust(wspace=0, hspace=0)
- In[6]과 같이 매번 바꿔서 보기가 귀찮다면, 이전에 배웠던 SubPlot을 활용해서 여러 변수들을 한 번에 Y변수인 MEDV와 비교할 수 있다.
- 결국 우리는 집값을 예측하고 싶기 때문에, 각 변수들과 MEDV의 상관관계를 눈으로 확인하고 싶은 것이고, 이를 위해 In[7]과 같이 X축을 CRIM, PTRATIO, AGE, NOX 등의 값을 지정하여 각각을 MEDV와 비교한 scatter plot을 그릴 수 있다.
- 좌하단에 있는 Age 그래프를 보면, Out[6]와 같은 그래프임을 확인할 수 있다.
- 좌상단의 CRIM(범죄율) 그래프를 보면 범죄율이 낮은 동네에는 비싼 집과 싼 집이 전부 존재하지만, 범죄율이 높아질수록 집값의 상한선이 정해지는 것 마냥 집값이 낮아지는 것을 볼 수 있다.
- 범죄율이 낮다고 무조건 집값이 비싸지는 것은 아니지만, 범죄율이 높으면 집값이 높아지긴 어렵다는 상관관계를 볼 수 있다.
- 마찬가지로 PTRATIO와 NOX를 보면서도 어떤 상관관계가 있는지 분석이 가능하다.
8. 여러 변수들 간(N:M)의 상관관계 분석
In [12]:pd.plotting.scatter_matrix(df_data[['CRIM', 'AGE', 'MEDV']],
diagonal='kde',
alpha=1 )
Out[12]:
- 이번엔 1:N이 아닌 N:M 비교를 해보자
- 꼭 Y변수와의 상관관계가 아니라 X1과 X2의 상관관계를 보고 싶을 때도 있기 때문이다.
- In[12]와 같이 df_data 중 비교하고 싶은 Series를 선택하면
- Out[12]와 같은 결과물이 생성된다.
- Out[12]의 대각선은 각 변수의 분포도이다
- [0][0] Index의 값은 CRIM 변수의 분포도이고, 3단계에서 봤듯이, 대부분의 값들은 0에 가깝고, 오른쪽으로 긴 꼬리가 생성되었음을 확인할 수 있다.
- [0][1]을 보면 x=age, y=crim 값을 갖는 분포를 표현했다. 어느 정도 연식까지는 범죄율과 상관관계가 거의 없이 낮은 듯 하지만, 그 정도를 넘어서는 순간 범죄율이 높아지는 상관관계를 볼 수 있다.
- 이렇게 다양한 변수들의 다자간 상관관계를 눈으로 보면, 당연하다고 생각되는 관계들이 대부분이지만, 간혹 아주 의외의 결과들도 확인할 수 있다.
9. N:M 다자간 상관도 분석 끝판왕 : Correlation Matrix
In [13]:corr_data = np.corrcoef(scale_data.T)
corr_data
Out[13]:array([[ 1. , -0.18292999, 0.39116137, -0.05222288, 0.41037672, -0.21543377, 0.34493361, -0.36652274, 0.60888632, 0.56652782, 0.27338389, -0.37016342, 0.43404449, -0.37969547],
[-0.18292999, 1. , -0.51333622, -0.03614653, -0.50228742, 0.31654961, -0.5412745 , 0.63838811, -0.30631636, -0.30833429, -0.40308541, 0.16743135, -0.40754907, 0.36594312],
...])
In [14]:corr_data.shape
Out[14]:(14, 14)
In [15]:fig = plt.figure(figsize=(10,10))
ax=fig.add_subplot(111)
cax = ax.matshow(corr_data, vmin=-1, vmax=1, interpolation='nearest')
fig.colorbar(cax)
ticks=np.arange(0,corr_data.shape[0],1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(df_data.columns)
ax.set_yticklabels(df_data.columns)
- 마지막 끝판왕은 Correlation Matrix이다
- In[13]에서 각 변수들 간의 상관계수를 계산한 뒤, 이를 그래프화하면 Out[15]와 같은 결과가 나온다.
'Python과 머신러닝 > MatPlotLib 데이터 시각화' 카테고리의 다른 글
| [Python.Seaborn] Seaborn 필수 그래프 정리 2 - Count Plot, Bar Plot, Dist Plot (0) | 2021.01.19 |
|---|---|
| [Python.Seaborn] Seaborn 필수 그래프 정리 1 - Line plot과 Scatter plot (feat. fmri & tips dataset) (0) | 2021.01.18 |
| [Python.MatPlotLib] Histogram과 Box Plot 그리기 (0) | 2021.01.05 |
| [Python.MatPlotLib] Scatter Plot 실습 (0) | 2021.01.04 |
| [Python.MatPlotLib] 그래프 꾸미기 III - 통신 데이터 분석 실습 (0) | 2021.01.03 |